瞭解雜訊的意義、新增位置,以及對評估作業的影響。
摘要報表是匯總可匯總報表的結果。 當收集器批次處理可匯總報表,並由匯總服務處理時,系統會在產生的摘要報表中加入隨機資料量,也就是雜訊。加入雜訊可保護使用者隱私。這項機制的目標是提供可支援差異隱私評估作業的架構。
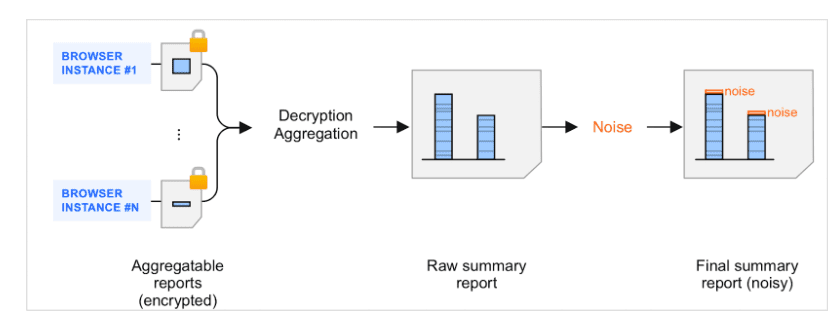
摘要報表中的雜訊簡介
雖然目前廣告評估通常不會加入干擾,但加入干擾後,您對結果的解讀方式在許多情況下不會有大幅改變。
不妨從以下角度思考:如果某項資料沒有雜訊,您是否會根據該資料做出決策?
舉例來說,如果廣告活動 A 有 15 次轉換,廣告活動 B 有 16 次轉換,廣告主是否會因此有信心變更廣告活動策略或預算?
如果答案為「否」,則雜訊與問題無關。
您需要設定 API 用量,確保:
- 答案是肯定的。
- 系統會以不致於大幅影響您根據特定資料做出決策的方式管理雜訊。您可以採取以下做法:針對預期的最低轉換次數,將收集到的指標中的干擾維持在特定百分比以下。
在本節和後續章節中,我們將概述達成目標 2 的策略。
核心概念
每次要求匯總報表時,匯總服務都會為每個摘要值 (也就是每個鍵) 新增一次雜訊。
這些雜訊值是從特定機率分布隨機抽取,如下所示。
影響噪音的所有元素都依賴兩個主要概念。
無論摘要值是低還是高,雜訊分布 (詳情請見下文) 都相同。因此,摘要值越高,相較於這個值,干擾的影響就越小。
舉例來說,假設總計 $20,000 美元的購買價值和總計 $200 美元的購買價值,都受到從相同分配選取的雜訊影響。
假設這個分布的雜訊大致介於 -100 和 +100 之間。
- 如果總購物價值為 $20,000 美元,雜訊的變動範圍介於 0 和 100/$20,000 美元=0.5% 之間。
- 如果總購買價值為 $200 美元,雜訊的範圍介於 0 和 100/200=50% 之間。
因此,與 $200 美元的價值相比,雜訊對 $20,000 美元匯總購物價值的影響可能較小。相對來說,20,000 美元的資料可能較少雜訊,也就是訊號雜訊比可能較高。
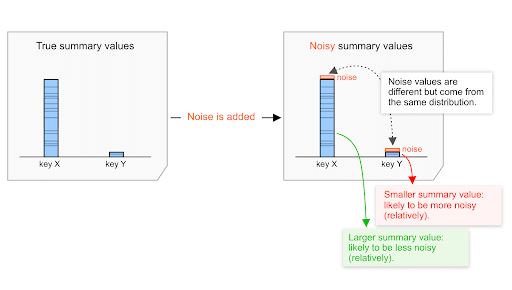
匯總值越高,雜訊影響就越小。 這會造成幾項重要的實際影響,詳情請見下一節。這項機制是 API 設計的一部分,實質影響是長期的。廣告技術人員設計及評估各種匯總策略時,仍會繼續發揮重要作用。
無論摘要值為何,系統都會從相同分布情形中抽出雜訊,但該分布情形取決於多個參數。其中一個參數 epsilon 可在來源試用結束前由廣告技術變更,以評估各種實用性/隱私權調整項目。不過,請將調整 epsilon 的功能視為暫時性功能。歡迎針對您的用途和適用的 epsilon 值提供意見。
廣告技術公司無法直接控管加入雜訊的方式,但可以影響雜訊對評估資料的影響。在接下來的章節中,我們將深入探討實務上如何影響雜訊。
在此之前,我們先來仔細看看套用雜訊的方式。
放大:套用雜訊的方式
一個雜訊分布
雜訊是從 Laplace 分布中抽出,參數如下:
- 平均值 (
μ) 為 0。也就是說,最有可能的雜訊值為 0 (未加入雜訊),且雜訊值小於原始值的機率與大於原始值的機率相同 (有時稱為「無偏」)。 b = CONTRIBUTION_BUDGET/epsilon的比例參數。CONTRIBUTION_BUDGET是在瀏覽器中定義的。epsilon用於匯總服務。
下圖顯示 μ=0、b = 20 的 Laplace 分布機率密度函式:
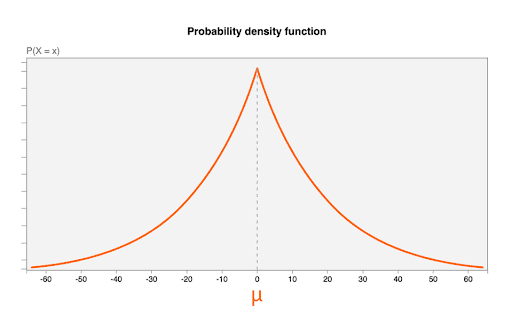
隨機雜訊值,一個雜訊分布
假設廣告技術為兩個匯總鍵 (key1 和 key2) 要求摘要報表。
匯總服務會選取兩個雜訊值 x1 和 x2,並遵循相同的雜訊分布。x1 會加到 key1 的摘要值,x2 則會加到 key2 的摘要值。
在圖表中,我們會將雜訊值視為相同。這是簡化說明,實際上,雜訊值會有所不同,因為這些值是從分配隨機抽取。
這表示雜訊值都來自相同分布,且與套用雜訊的摘要值無關。
噪音的其他特性
系統會對每個摘要值套用雜訊,包括空值 (0)。
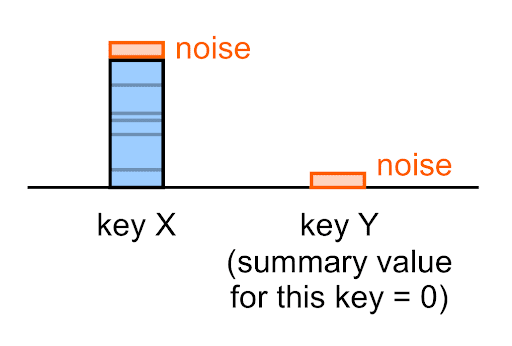
舉例來說,即使特定鍵的真實摘要值為 0,您在該鍵的摘要報表中看到的雜訊摘要值 (很可能) 不會是 0。
雜訊可以是正數或負數。
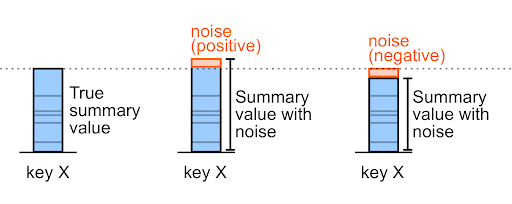
舉例來說,假設加入干擾前購買金額為 327,000,干擾可能是 +6,000 或 -6,000 (這些是任意範例值)。
評估噪音
計算雜訊的標準差
噪音的標準差為:
b*sqrt(2) = (CONTRIBUTION_BUDGET / epsilon)*sqrt(2)
範例
如果 epsilon = 10,雜訊的標準差為:
b*sqrt(2) = (CONTRIBUTION_BUDGET / epsilon)*sqrt(2) = (65,536/10)*sqrt(2) = 9,267
評估評估差異是否顯著
由於您會知道匯總服務為每個值輸出內容新增的雜訊標準差,因此可以判斷適當的比較門檻,藉此判斷觀察到的差異是否可能歸因於雜訊。
舉例來說,如果加到值中的雜訊約為 +/- 10 (考量縮放),且兩個廣告活動之間的值差異超過 100,則可安全地推斷,每個廣告活動之間測得的值差異並非單純由雜訊造成。
參與討論及分享意見
歡迎參與並試用這項 API。
後續步驟
- 如要瞭解可控制哪些變數來改善訊號雜訊比,請參閱「處理雜訊」。
- 如需規劃匯總報表策略的相關協助,請參閱「實驗:摘要報表設計決策」。
- 試試噪音實驗室。

